Tiempo, Espacio y Materia...

Tiempo, espacio y materia

Problemas Propuestos: 1)- Cual es el tiempo que requiere una emisora que trasmite a 91.3 MHz para enviar una onda? 2)- Si un martillo golpea 65 veces en 5.00 s ¿Cual es el tiempo de un martillazo? ¿Cuántas veces golpea el martillo cada segundo? Otro sencillo, aquí preguntan tanto como el periodo (T), como por la frecuencia (F). 3)- Si un motor gira a 1600 rpm ¿Cual es su periodo? 4)- Un estudiante lanza una visual hacia la azotea de un edificio con un Angulo de elevación de 23.4 grados. La base del edificio está a 136 m del observador. Desprecie la altura del estudiante y determine la del edificio. 5)- Dos edificios están separados por 253 m y tienen alturas diferentes. Un observador se coloca en la azotea del edificio A y mira la azotea del edificio B con un Angulo de depresión de 53.2o . Luego observa la base del edificio B con una visual que forma un ángulo de 23.2o con respecto a la vertical, determine la altura de ambos edificios. 6)- ¿En cuanto deberá aumentar el radio de un círculo si se desea triplicar su área? 7)- El volumen de un cilindro es 2.00 x103 cm3 si se reduce su radio a la tercera parte para obtener otro cilindro semejante, ¿Cuál deberá ser el volumen del nuevo cilindro? 9)- La relación entre las áreas de dos triángulos semejantes es A2=9A1. Encuentre la relación entre sus alturas. 10)- Si el diámetro de un circulo se reduce a la quinta parte ¿En cuanto se reducirá su área? 11)- Halle el volumen barrido por un triangulo rectángulo cuando este gira 60º en torno a su cateto mayor. Los catetos miden 8.00 cm y 6.00 cm. 12)- Halle la densidad de 5 galones de aceite, si 50.00 ml de aceite tienen una masa igual a 38.0 13)- Un prisma tiene 100 cm3 de capacidad, si se cuadruplicara su altura para obtener otro semejante ¿Cuál será su nuevo volumen? ¿En cuánto aumentara su área? Solución de los problemas propuestos 1)------------------------------------------------------------------------------------------------------- Este es un tipo problema de 5 puntos en el primer parcial, generalmente nunca se queda. Es muy sencillo: El problema pregunta por el tiempo que envía una onda, esto se refiere al periodo (T), Tiempo en que ocurre un evento. Datos: F= 91.3 x106 (M=x10 6) Hz Formulas posibles: F=1/T F=n/t T=t/n T=1/F Solución: T=1/F T=1/91.3 x106 Hz T=1.10 x10-8 segundos 2)----------------------------------------------------------------------------------------------------- Otro sencillo, aquí preguntan tanto como el periodo (T), como por la frecuencia (F). T=t/n = 5.00 s/65 = 0.0769 s F=n/t = 65/5.00 s = 13.0 s-1 (s -1 = Hz) 13 martillazos cada segundo. Otra forma: F=1/T = 1/0.0769 = 13.0 3)----------------------------------------------------------------------------------------------------- En este problemita muchos estudiantes se "trancan" y no se imaginan lo fácil que es. Datos: Sabemos que son 1600 (r) por minuto (60 s) Las revoluciones serán n y el minuto pues los 60 segundos T=t/n = 26.7 s Para los problemas antes dados: Error frecuente es confundir las formulas ya que son parecidas pero NO iguales. También otro error es decir el periodo de 1600 rpm es 1/1600, esto es un completo error ya que el resultado va a ser en minutos y no en segundos. LAS REVOLUCIONES SON n.... 4)---------------------------------------------------------------------------------------------------   Simple: Un poco de relaciones trigonométricas: tang ángulo= op/ad tan23.4o= h/136 m (136m)(tan23.4o)=h 58.8 m= h 5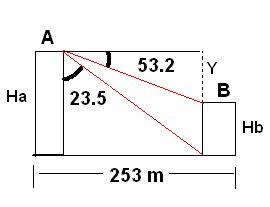)------------------------------------------------------------------------------------------------- Determinar la altura del edificio A: Ha= Altura del edificio A Tan 23.5o = 253 m/Ha Ha= 253 m/Tan 23.5o Ha= 582 m Determinar altura del edificio B: Primero determinaremos cuánto mide la línea punteada: Altura de línea punteada = Y Tan 53.2o = Y / 253 m (se puede apreciar que es la misma distancia) 253 m (Tan 53.2) = Y Y = 338 m Ahora bien, ¿Cómo determinaremos la altura del edificio B? Sabemos la altura del A y sabemos una longitud la cual no pertenece al B, por esto solo debemos restar la altura del A con la de la línea punteada y nos dará la altura del B. Ha-Y = Hb 582 m-338 m = 244 m (Recuerda que para sumar deben tener la misma cantidad de cifras significativas después del punto). Hb= 244 m La triangulación es un método que con saber razones trigonométricas prácticamente se resuelven. Un problema común es que cogen el ángulo con la vertical, solo se pone con la vertical cuando el mismo ejercicio lo dice, de otra manera si solo dice “lanza una visual a 23.4o” se asume que es con la horizontal. Los problemas de triangulación siempre van a ser con razones trigonométricas, o sea que siempre van a formar triángulos rectángulos. La triangulación es un posible punto de 25 en el primer parcial. 6)-------------------------------------------------------------------------------------------------------- A2=n2A1 A2=3A1 (Solo es la representación del problema) Como queremos saber en cuanto deberá aumentar una dimensión lineal en este caso el radio, solo hay que sacarle la raíz cuadrada a 3, ya que estamos hablando de áreas y las áreas poseen 2 dimensiones. R2=1.41 R1 Cuando se pregunta por una dimensión lineal con respecto al área hay que sacar raíz cuadrada pero cuando se pregunta por la relación de las áreas con respecto a una dimensión lineal hay que elevar al cuadrado. Para los volúmenes es igual pero envés la raíz cuadrada es cubica al igual que el exponente. 7)-------------------------------------------------------------------------------------------------------- N=1/3 R2=1/3R1 V2=n3V1 (Recuerda que se eleva al cubo porque es volumen) V2= (1/3)3V1 V2= (1/27)V1 V1 = 2.00 x103 cm3 V2= 2.00 x103 cm3 / 27 V2= 74.1 cm3 8)--------------------------------------------------------------------------------------------------------- A= (¾) de circulo El área del circulo es (3.1416)(R)2 A= (3.1416)(18.5 cm)2 A = 806 cm2 (es cm2 porque es el área (2 dimensiones)) 9)--------------------------------------------------------------------------------------------------------- A2=9A1 A2=n2A1 A2=9A1 H2= (raíz cuadrada de 9) H1 H2= (3) H1 10)----------------------------------------------------------------------------------------------------- N= 1/5 D2= (N) D1 D2= (1/5) D1 A2= (n)2 A1 A2= (1/5)2 A1 A2= (1/25) A1 11)----------------------------------------------------------------------------------------------------- Para que proporción de volumen barrio dividimos 60/360 = 0.167 Cuando el triangulo rectángulo gira forma una parte de un cono. La altura de este cono va hacer igual al cateto por donde gira el triangulo. V de un cono= (1/3) (3.1416)(h)(R)2 V barrido = (0.167)(1/3) (3.1416)(h)(R)2 V barrido = (0.167)(1/3) (3.14)(8.00 cm)(6.00 cm)2 V barrido = 50.3 cm3 12)----------------------------------------------------------------------------------------------------- P= M/V P=38.0 g/ 50.0 ml = 0.760 g/cm3 Ml = cm3 La densidad es una propiedad de un cuerpo, la densidad de 5 galones de aceite es la misma que la de una gota de aceite ya que es el mismo aceite. Hay que tener en cuenta que la densidad se mide en g/cm3 y en kg/ m3 es incorrecta la expresión g/m3 o kg/cm3. 13)----------------------------------------------------------------------------------------------------- N= 4 V2= (4)3V1 V2=64 V1 V2=64 (100 cm3) V2= 6.40 x 103 cm3 ---------------------------- A2=(4)2A1 A2=(16)A1 Si quieres puedes enviar ejercicios a [e-mail]